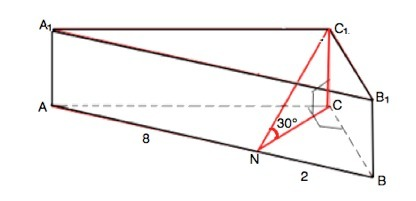
Объём призмы равен произведению её основания и высоты. Судя по данным условия, призма прямая с прямоугольными треугольниками в основаниях.
Угол СNВ=90°⇒ СN - высота основания.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками, на которые она её делит:
СN=√AN•BN=√8•2=4
Высота призмы СС1=NC•tg30°=4/√3
S(ABC)=0,5•CN•(AN+BN)=20
V(призмы)=20•4/√3=80/√3 ед. объёма.