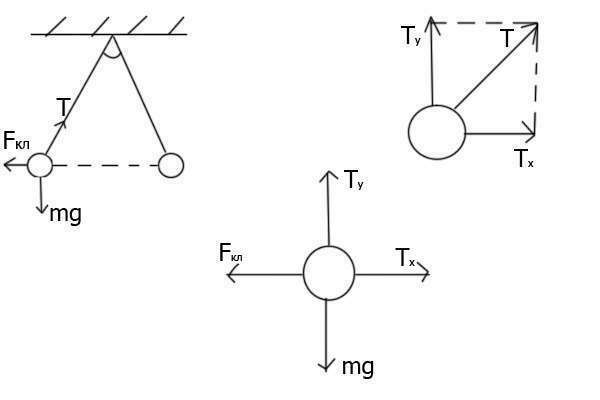
Сначала покажем все силы, которые действуют на шарики. Они похожи, поэтому нарисовано только на одном шарике. Разложим силу натяжения нити по осям Ox и Oy:
1) Ty = T*cos60
2) Tx = -T*sin60
Т. к. шарики находятся в состоянии покоя, то силы компенсируют друг друга, т. е.
3) Ty = Fкл
4) Tx = mg
По формуле находим:
Fкл = 
r - расстояние между шариками, т. к. треугольник у нас равнобедренный ( по 20 см боковые стороны) и угол при вершине 60, то наш треугольник - равносторонний. r = 20
Выразим, чему равно Т из 1-го уравнения и 3-го.
T = 
= 
= 0,072 H
Теперь, зная уравнение 4 и 2, находим массу:
m = Tx/g = 
= 6,36*
кг = 6,36 г
P. S. cos60 = 1/2, sin60 = 
/2
Минус в расчете массы идет потому, что взят он из уравнения 2, а направление силы тяжести идет вниз
