Помогите решить задачу: образующая конуса равна l, а радиус основания равен r. Найдите...

Question

Помогите решить задачу: образующая конуса равна l, а радиус основания равен r. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу: а) в 60°; б) в 90°.
Обязательно с рисунком , дано и с подробным решением!!!!!!!!!!
Помогите, пожалуйста))))

Answer 1

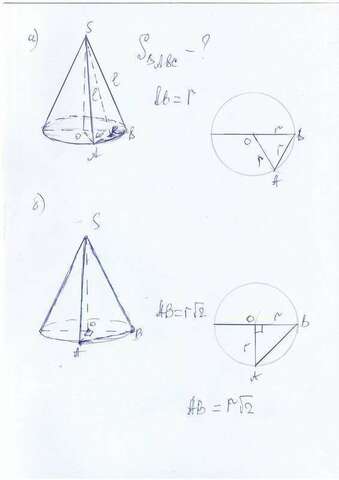
A) Дано: конус, АВ=l,  OA=OB=r,  АВ - хорда, ∠BOA=60°
найти: S ΔAOB
Решение:
SΔ = 1/2*a*h = 1/2*AB*SK
AB= r. SK ищем из ΔАSK по т Пифагора:
SK² = l² - (r/2)² = l² - r²/4= (4l² -r²)/4
SK = √(4l² - r²) /2
S сеч. = 1/2*r*√(4l² - r²) /2 = r*√(4l² - r²) /4
б)  Дано: конус, АВ=l,  OA=OB=r,  АВ - хорда, ∠BOA=60°
найти: S ΔAOB
Решение :
SΔ = 1/2*a*h = 1/2*AB*SK
АВ ищем из ΔАВО по т. Пифагора: АВ² = r² + r² = 2r², AB = r√2
SK ищем из ΔАSK по т Пифагора:
SK² = l² - (r√2/2))² = l² -2 r²/4= (4l² -2r²)/4
SK = √(4l² -2 r²) /2
S сеч. = 1/2*r*√(4l² -2 r²) /2 = r*√(4l² -2 r²) /4

---

Comments

б)  Дано: конус, АВ=l,  OA=OB=r,  АВ - хорда,   ∠BOA=60°  (COPY-PASTE)  ; ∠BOA=90°   

Answer 2

Рассмотрим основание:в образованном треугольнике MON: OM = ON как радиусы, следовательно, треугольник равнобедренный, угол MON = 60 градусов по условию, углы OMN и ONM равны как углы равнобедренного треугольника по основанию, то есть Аналогично по первому решению, во втором случае углы OMN и ONM = (180 - 90)/2 = 45 градусов. Тогда по теореме синусов: MN/sin90 = ON/sin45, MN = корень из 2 умножить на r. Из треугольника CON: CO = корень из (l^2 - r^2). Площадь второго треугольника равна r умножить на корень из (4*l^2 = 2r^2)/2) поделить на 2.

---

---

---

---

---