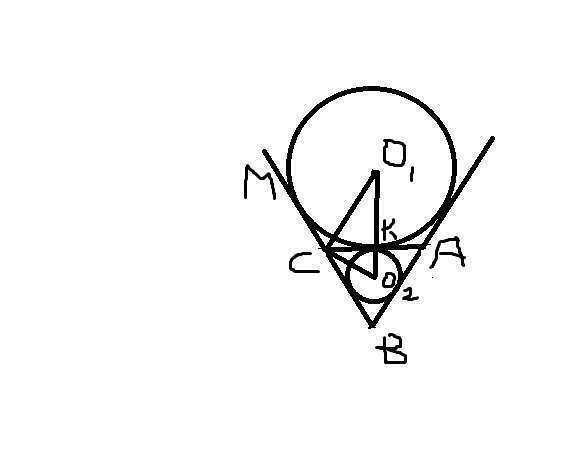
Центр окружности, которая касается двух пересекающихся прямых, лежит на биссектрисе угла между ними. Поэтому СО₁ и СО₂ - биссектрисы углов ВСК и МСК. Эти углы - смежные, их сумма 180°⇒∠О₁СО₂=90°. ΔСО₁О₂ - прямоугольный. Точки О₁, К, О₂ - лежат на биссектрисе угла В. В равнобедренном треугольнике биссектриса, проведенная к основанию, является высотой.⇒СК⊥О₁О₂. По теореме о среднем пропорциональном в прямоугольном треугольнике
СК² =КО₂*КО₁.
СК=2, КО₁=4
КО₂=СК²/КО₁=2²/4=1. А для боковой стороны писать очень долго, там и подобие и теорема Пифагора. Получился ответ 3цел1/3.