Помогите пожалуйста кто сможет)) Сколько корней имеет уравнение зависимо от параметра а?

Рассмотрим функции $f(x)=(x-1)(4-|x|)$ и $g(x)=a$
Пусть $y(x)=x-1$ и $4-|x|=k(x)$ , причем это функции
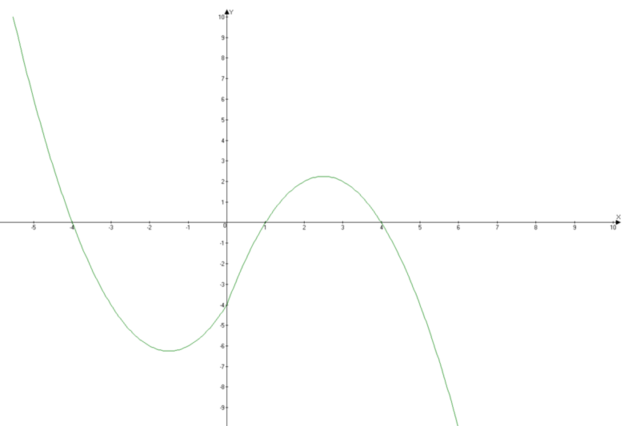
Построим графики y(x) и k(x).
$y(x)=x-1$ - прямая, проходящая через точки (0;-1), (-1;-2), (1;0), (2;1), (-2;-3)
$k(x)=4-|x|$ - прямая, проходящая через точки (0;4), (-1;3), (1;3), (2;2), (-2;2)

В умножение графиков $f(x) = y(x)\cdot g(x)$ абсциссы должны быть равны. Первую координату оставляем, а ординату графиков функций y(x) и k(x) прибавляем, тоесть:

(0;3), (-1;1), (1;3), (2;3), (-2;-1) - точки умножения графиков y(x) и k(x)

$g(x)=a$ - прямая, параллельная оси Ох

Вывод:
При $a=-6,25$ и $a=2,25$ уравнение имеет 2 корня
При $a \in (-\infty;-6.25)\cup(2.25;+\infty)$ уравнение имеет 1 корень
При $a \in (-6.25;2.25)$ уравнение имеет 3 корня