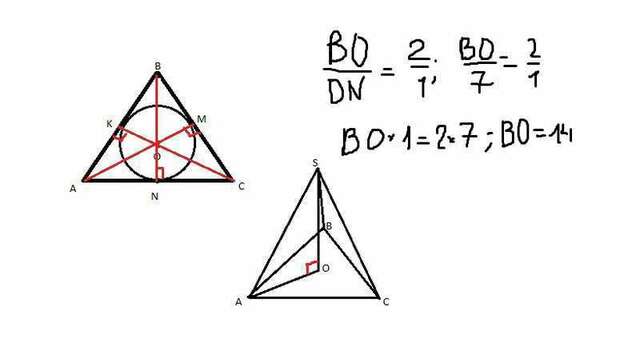Задача 3. Правильная треугольная пирамида - это пирамида, в основании которой лежит правильный треугольник. Рассмотрим основание пирамиды SABC: в треугольнике ABC: AM = BN = CK - медианы треугольника, а поскольку треугольник правильные, они же являются биссектрисами и высотами. Исходя из свойства медиан, которые пересекаются в одной точке, которая делит их в отношении 2:1, считая их от вершины. Имеем: BO:ON = 2:1, ON - радиус, следует, BO:7 = 2:1; из пропорции находим BO = 2/1*7, BO = 14.
Рассмотрим треугольник SOA: поскольку SO - высота, то угол SOA = 90 градусов; SA = 50 по условию, AO = CO = BO = 14, исходя из вышеизложенного. Из прямоугольного треугольника SOA: из теоремы Пифагора: SO^2 = SA^2 - AO^2, SO^2 = 50^2 - 14^2, SO^2 = 2500 - 196 = 2304, SO = корень из 2304, SO = 48.
Ответ: высота пирамиды равна 48 единиц.
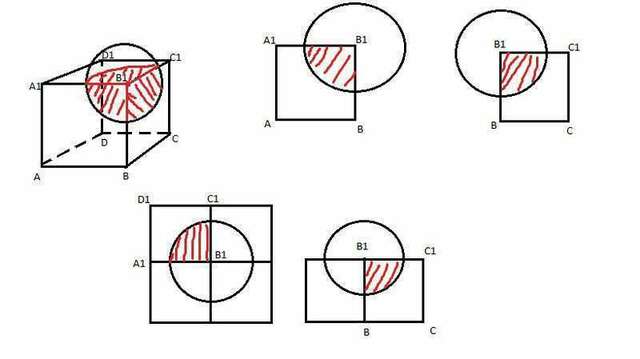
Задача 4. Здесь без пространственного воображения не обойтись. Из рисунка два видно, что площадь нужного нам шарового сегмента шара, который находится внутри куба, равна 1/4 половины площади поверхности шара, то есть, 1/8 площади поверхности всего шара. Площадь полной поверхности шара S = 4*pi*R^2 = 4*1,5^2*pi = 9*pi единиц. Имеем: площадь нужной поверхности шара равна: S = (9*pi)/8.
Ответ: поскольку ответ нужно записать в S/pi, то ответом будет число (9*pi)/8*pi = 9/8 единиц.