Y= 5-корень10x^2-18x+8Найдите наибольшеее значение функции.При каких значениях x оно...

$y=5-\sqrt{10x^2-18x+8}$

$y-5=-\sqrt2\cdot \sqrt{5x^2-9x+4}\; \; \to \; \; y-5\ \textless \ 0,\; y\ \textless \ 5\\\\5x^2-9x+4=5(x^2-\frac{9}{5}x)+4=5((x-\frac{9}{10})^2-\frac{81}{100})+4=\\\\=5(x-0,9)^2-\frac{81}{20}+4=5(x-0,9)^2-0,05\\\\y-5=-\sqrt2\cdot \sqrt{5(x-0,9)^2-0,05}\\\\(y-5)^2=2\cdot (5(x-0,9)^2-0,05)\\\\(y-5)^2=10(x-0,9)^2-0,1\\\\10(x-0,9)^2-(y-5)^2=0,1\. |:0,1\\\\\frac{(x-0,9)^2}{0,01}-\frac{(y-5)^2}{0,1}=1$

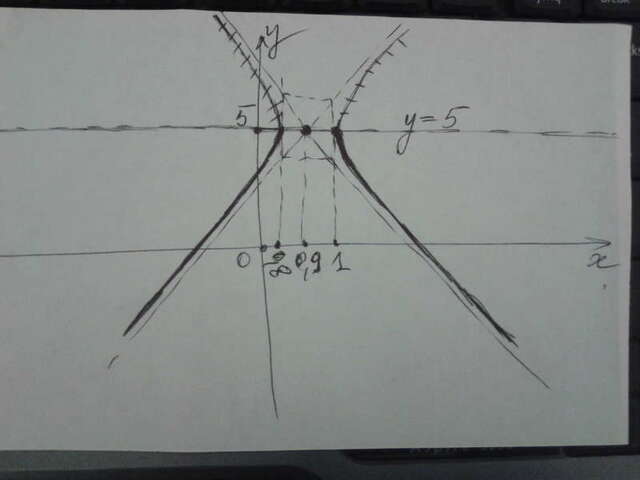
Это уравнение гиперболы с центром в точке (0,9 ; 5).
Её ось симметрии прямая у=5. Вершины имеют координаты
(0,8 ; 5) и (1,5), так как параметры гиперболы: а=0,1 и b=√0,1~0,32.

Изначально было задано уравнение не всей гиперболы,
а только её часть, расположенная ниже прямой у=5 (y<5).<br>Наибольшее значение будет достигаться в вершинах
гиперболы, так как верхние ветви в график не входят.
Итак, наибольшее значение функции у=5, и достигается оно
при х=0,1 и при х=√0,1.