1) Найти ООФ
2) Если есть точки разрыва, исследовать их
Эти 2 вопроса практически совпадают, так как ООФ включает точки разрыва:
Если переменная в знаменателе, то есть точки разрыва при знаменателе, равном 0.
5 - 3х² = 0,
х = +-√(5/3),
значит, точки разрыва х₁ = -√(5/3) = -1.290994, х₂ = √(5/3) = 1.290994.
То есть график функции разбит на 3 участка:
первый от-∞ до -√(5/3),
второй от-√(5/3) до √(5/3),
третий от √(5/3) до +∞.
3) Найти точки пересечения с осями координат:
С осью У при Х = 0
у = х³ - 5х = 0,
Отсюда одно значение у = 0.
С осью Х при У = 0
Дробь равна 0, когда числитель равен 0
х³ - 5х = 0,
х(х² - 5) = 0
х₁ = 0,
х = +-√5,
х₂ = -√5 = -2.2360679,
х₃ = √5 = 2.2360679.
4) Вычислить чётность/нечётность:
f(-x) = ((-x)³ - 5(-x)) / (5 - 3(-x)) = -(x³ - 5x) / (5 - 3x²).
То есть f(-x) = -f(x).
Значит, функция нечётная.
5) Выяснить периодичность - нет периодичности.
6) Найти производную, промежутки монотонности функции, экстремумы:
Производная\:частного: 
После подстановки получаем
Знаменатель производной в квадрате всегда положителен.
В числителе переменная в чётной степени, а выражения с минусом.
Значит, на каждом промежутке функции она убывающая.
Производная не может быть равна 0 (из за наличия переменной в знаменателе), поэтому у функции нет ни максимума, ни минимума.
7) Найти промежутки выпуклости, вогнутости, вторую производную и точки перегиба:
для этого надо найти вторую производную:
– если вторая производная меньше 0 на интервале, то график функции является выпуклым на данном интервале;– если вторая производная больше 0 на интервале, то график функции является вогнутым на данном интервале.
Вторая производная равна:
Нулю может быть равна только при х = 0.
Это одна точка перегиба.
В точках разрыва функция меняет выпуклость на вогнутость, но это не считается точкой перегиба, так как функция в этих точках не определена.
8) Асимптоты графика функции (y=kx+b)
Есть 2 вертикальные асимптоты в точках разрыва х₁ = -√(5/3) и х₂ = √(5/3).
уравнение наклонной асимптоты слева:
y = -х / 3,
справа уравнение наклонной асимптоты такое же:
y = -х / 3.
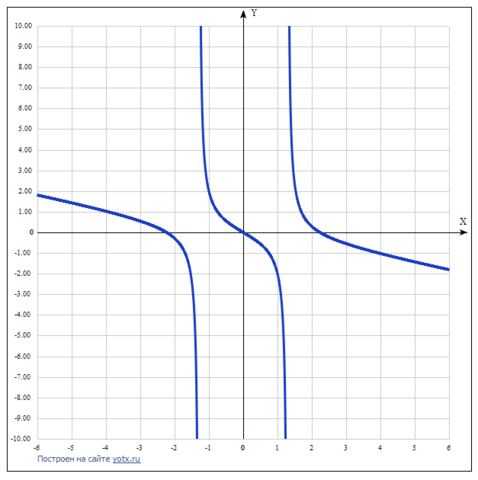
9) Построить график. Смотри приложение.
