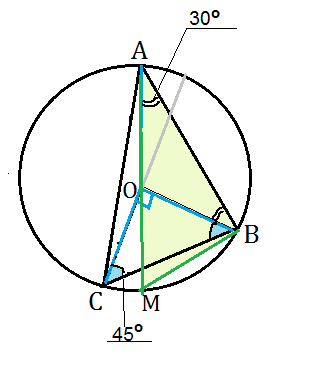
Окружность в центре О и радиусом 16 см описана около треугольника АВС так, что угол ОАВ =30 градусов, угол ОСВ=45 градусов. Найти АВ и ВС в треугольнике АВС.
------------
Продолжим АО до пересечения с окружностью в точке М
Соединим М и В.
АМ - диаметр и равен 2 R=32 см,
∠АВМ=90º - опирается на диаметр.
В ∆ АВМ- ∠ АМВ=90º-30º=60º.
АВ=АМ*sin60º=32*√3):2=16√3 (см) или по т. Пифагора
ВМ=АМ:2=16 ( лежит против угла 30º)
АВ=√(АМ²-ВМ²)= 16√3 см
∆ ВОС - равнобедренный, образован двумя радиусами СО=ВО и гипотенузой ВС.
Т.к. угол ОСВ=45º, второй острый угол ОВС=45º, угол СОВ=90º
По т. Пифагора СВ=CO√2=16√2 см
Ответ:ВС=16√2 см; AB=16√3 см