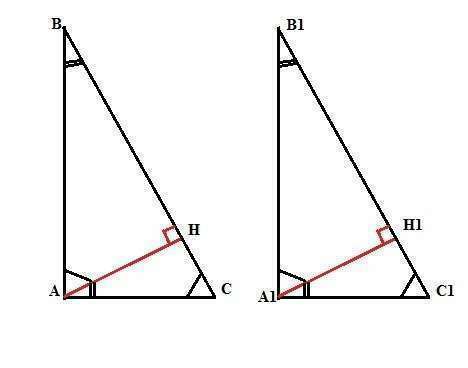
Пусть даны два прямоугольных треугольника АВС и А1В1С1, у которых <А=<А1=90°, <C=<C1 и высоты АН и А1Н1 равны.<br>Тогда и Высоты АН и А1Н1 делят треугольники АВС и А1В1С1 на подобные.
Значит a Значит Тогда прямоугольные треугольники АВН и А1В1Н1 равны по катету (АН=А1Н1 -дано) и прилежащему острому углу (Прямоугольные треугольники АСН и А1С1Н1 равны по катету (АН=А1Н1 -дано) и прилежащему острому углу (<СAH=<С1A1H1). Значит СН=С1Н1.<br>ВС=ВН+СН, В1С1=В1Н1+С1Н1. Отсюда ВС=В1С1.
Гипотенузы треугольников ВС и В1С1 равны, острые углы их тоже равны, значит треугольники АВС и А1В1С1 равны по равенству гипотенузы и острому углу (третий признак).
Что и требовалось доказать.