[[ I ]]
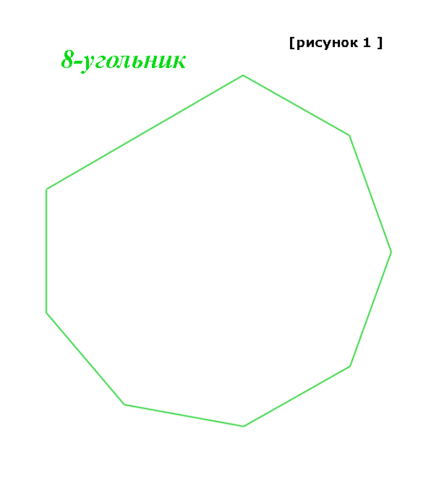
Для начала, нам потребуется рассмотреть точки выпуклого восьмиугольника (!), при этом неважно – правильный он или нет, главное, чтобы он был – выпуклый. Рисунок 1.
Кроме того, рассмотрим все ломанные, а не только несамопересекающиеся, т.е. и замкнутые и, возможно, самопересекающиеся.
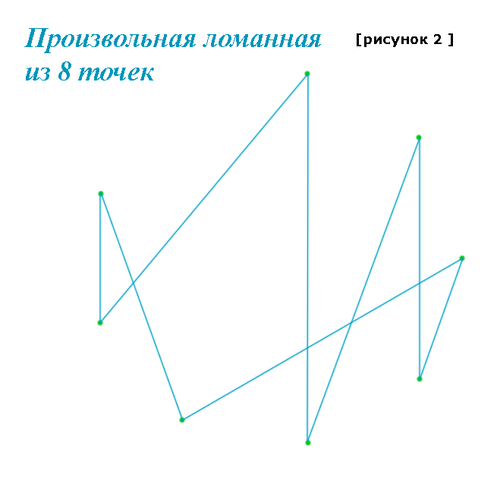
Нарисуем произвольную ломанную. Получим конструкцию, в которой каждая точка лежит на конце двух отрезков, поэтому на всех точках кончается 16 отрезков, однако, поскольку каждый отрезок кончается на двух точках, то значит всего отрезков в такой конструкции ровно 8. Такая конструкция будет представлять собой замкнутую и, возможно, самопересекающуюся восьмизвенную (!) ломанную. Рисунок 2.
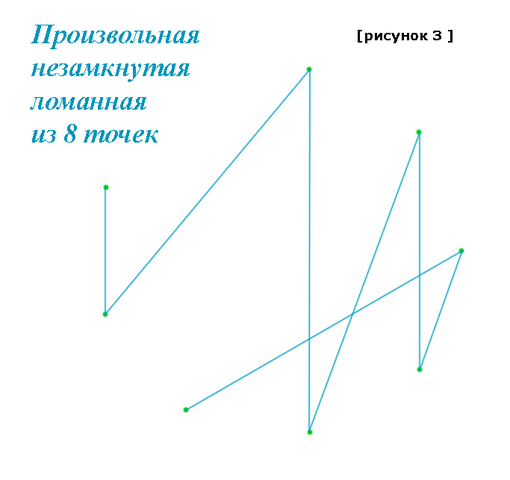
Теперь сотрём один из отрезков этой неправильной ломанной и получим НЕЗАМКНУТУЮ, но, возможно, самопересекающуюся ломанную у которой как раз 7 звеньев ! Рисунок 3.
Значит, если из 8 точек: в 6 провести по два отрезка, а на двух остальных окончить только по одному отрезку – то получается 7-звенная ломаная, правда, возможно самопересекающаяся.
Т.е., если все из 8 (!) точек использовать, то получается как раз семизвенная незамкнутая ломанная. Как же её построить так, чтобы она не имела самопересечений?
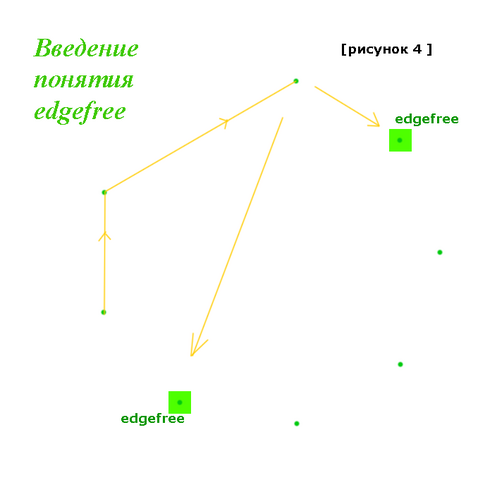
Введём в рассуждение такой термин – edgefree (крайняя-свободная), и поясним, что он означает. Рисунок 4. Пусть уже какое-то количество точек использовано в ломанной, и мы стоим перед выбором, куда провести следующее звено, и перед нами есть, например 5 точек. Встанем к использованным трём точкам "задом", а к неиспользованным "передом". Все они перед нами будут, как под прицелом – расположенные в некоторой последовательности. Крайняя по левую руку и крайняя по правую и будут – точками edgefree.
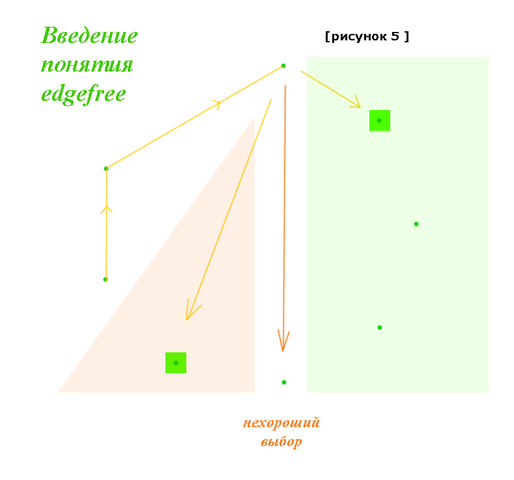
Если дальше мы выберем не edgefree, а какие-то другие точки (рисунок 5), то следующим звеном мы разделим всё множество оставшихся точек на 2 группы: те, что слева от новой точки (зелёная область), и те, что справа (красная область). И проведя такое новое неправильное звено, попадём в ловушку, так как нам нужно будут использовать все точки и из левой и из правой групп, а сделать это, не пересекая последнее проведённое нами звено, будет уже невозможно.
Значит, каждый раз, при построении 7-звенной ломанной в выпуклом восьмиугольнике (!), у нас есть только две возможности выбрать следующую точку: левая или правая edgefree. Важно отметить, что когда выбрано уже 7 точек в восьмиугольнике – остаётся только одна точка (!), она, конечно же, edgefree точка, но она только одна (!) и выбрать её из двух вариантов уже нельзя.
Учитывая всё сказанное, получаем:
1. Первую точку можно выбрать 8-мью способами.
2. Вторую точку можно выбрать 2-мя способами.
3. Третью точку можно выбрать 2-мя способами.
. . .
6. Шестую точку можно выбрать 2-мя способами.
7. Седьмую точку можно выбрать 2-мя способами.
8. Восьмую точку можно выбрать только одним способом, т.к. она единственна.
Значит всего несамопересекающихся незамкнутых семизвенных ломанных в восьмиугольнике (!) можно провести: 
способами. Однако, поскольку у ломанной два конца, то будут получаться "парные" одинаковые ломанные, у которых голова и хвост поменяны местами.
В итоге получаем: 
вариантов.
[[ II ]]
Теперь, чтобы решить исходную задачу, вычеркнем из 9 заданных точек одну! И мы как раз получим 8 точек, на которых будет расположен выпуклый восьмиугольник. Всего из девятиугольника можно вычеркнуть одну точку 9-ью способами.
Поэтому окончательный ответ должен быть в 9 раз больше вычисленного в пункте [I]. Всего 
способов провести семизвенную несамопересекающуюся ломаную.
О т в е т : 
