17 БАЛЛОВ!РЕШИТЕ МНЕ ЭТО! Постройте график функции y=(x➃-5x➁+4)/(x+1)(x-2) и...

Question

17 БАЛЛОВ!
РЕШИТЕ МНЕ ЭТО!
Постройте график функции y=(x➃-5x➁+4)/(x+1)(x-2) и определите,при каких значениях c прямая y=с имеет с графиком функции только одну общую точку.

Answer 1

Числитель - это биквадратный многочлен. Его можно разложить на множители:
Заменим х² = у.
Получаем квадратный трёхчлен: у² - 5у + 4. Приравняем его нулю.
у² - 5у + 4 = 0.
Квадратное уравнение, решаем относительно y: 
Ищем дискриминант:D=(-5)^2-4*1*4=25-4*4=25-16=9;
Дискриминант больше 0, уравнение имеет 2 корня:
y_1=(2root9-(-5))/(2*1)=(3-(-5))/2=(3+5)/2=8/2=4;
y_2=(-2root9-(-5))/(2*1)=(-3-(-5))/2=(-3+5)/2=2/2=1.
Отсюда х = +-2   и х = +-1.
Числитель приобретает вид (х+1)(х-1)(х+2)(х-2).
После сокращения у = (х-1)(х-2).
Это даёт 2 корня: х = 1  и х = 2.
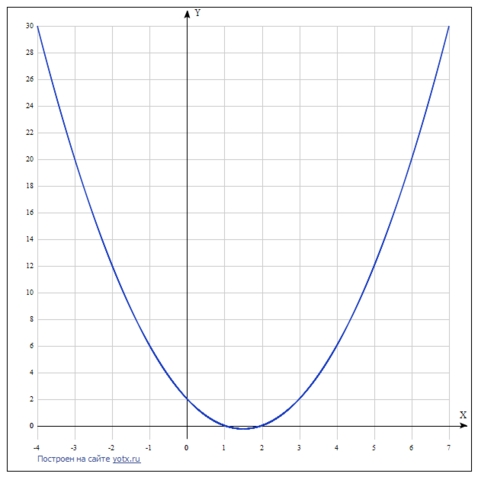
График - парабола у = х² - 3х + 2.
Осталось найти касательную, проходящую через начало координат.
Примерно, это у = -5,8х.

---

Comments

Дополнение к ответу: Производная заданной функции f'=2x-3. Уравнение касательной Ук=f(Xk)+f'(xk)*(X-Xk). Подставим в уравнение: Yk=Xk^2-3Xk+2+(2Xk-3)*(X-Xk) Раскрыв скобки и приведя подобные, получаем уравнение касательной: Ук=(2Хк-3)*Х+(-Хк^2+3). Чтобы уравнение её было вида У = сХ, выражение (-Xk^2+2) должно быть равно нулю.

---

Отсюда Хк = +-корень из 2. Тогда в коэффициент перед "Х" подставляем полученные значения точки, в которой производная проходит через начало координат. Получаем 2 значения: а = -0,17157 и а = -5,82843. 

---

Но в условии задания требуется найти значение "с" прямой у = с. Это прямая, параллельная оси Х и являющаяся касательной к параболе в её вершине. Хо = -в / 2а = 3 / 2. Отсюда У =(9/4)-(3/2) +2 = (-1/4). Это и есть значение "с".