Сторона параллелограмма AB равна с диагональю BD, длина которой 15 см, сторона AD равна...

Question

Сторона параллелограмма AB равна с диагональю BD, длина которой 15 см, сторона AD равна 24 см.

1. Определи площадь параллелограмма:??
2. Сколько видов решений можно применить для определения площади?

1формулу площади параллелограмма - умножение высоты и стороны
2формулу умножения диагоналей
3формулу Герона
4формулу умножения сторон и синуса угла между ними

Answer 1

1) S=h•a

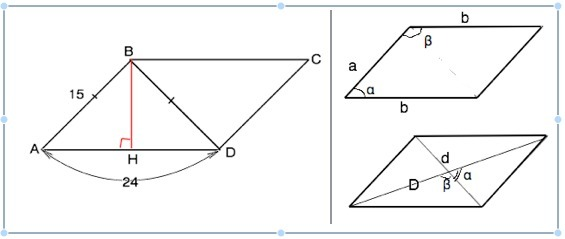
∆ АВD равнобедренный. Высота ВН - его медиана. 

АН=DH=12

Высота по т.Пифагора 

ВН=√(АВ²-АН²)=√(225-144)=9

S=9•24=216 см²

2) Для определения площади параллелограмма можно применить формулы:

а) Умножения высоты и стороны:  S=h•a

б) Формулу Герона S=√p(p-a)(p-b)(p-c) для половины параллелограмма и последующего умножения на 2.

в) Формулу умножения сторон и синуса угла между ними: S=a•b•sinα=a•b•sinβ

--

Что касается формулы умножения диагоналей, то правильной будет Формула площади параллелограмма через диагонали и угол между ними:

S=0,5•D•d•sinα=0,5•D•d•sinβ

---