2cosx=√3
Разделим обе части уравнения на 2, чтобы избавиться от коэффициента при косинусе:
cosx=√3/2
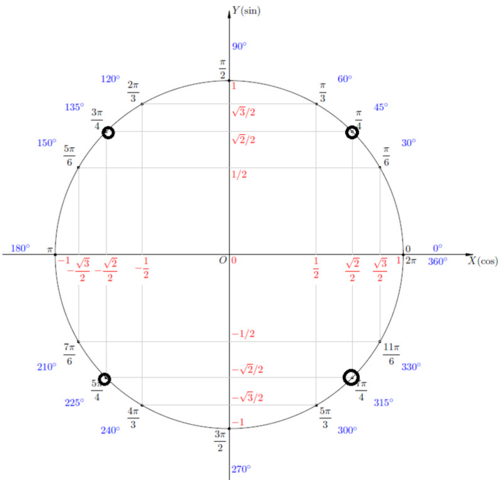
Теперь откройте рисунок. На нём изображён тригонометрический круг. Находим по тригонометрическому кругу, где значение косинуса достигает √3/2. На самом деле, все мы учили таблицу значений косинусов и синусов (я тоже её Вам отправляю картинкой), просто тригонометрический круг объясняет, почему именно данному углу принадлежит то или иное значение косинуса или синуса. Хочу заметить, что косинус откладывается по оси "х".
Итак, значение косинуса √3/2 соответствует углу в 30 градусов, т.е. углу π/6. Можно подумать, что мы нашли ответ. На самом деле мы не совсем нашли ответ. Смотрим, при прохождении полного круга 2π мы попадаем в эту же точку, где косинус так же равен √3/2, но угол уже будет другой: π/6 + 2π=13π/6. И когда мы ещё раз пройдём по кругу будет уже другой угол, больше (если прибавляем 2π) или меньше (если отнимаем 2π) всё с тем же значением косинуса √3/2.
Поэтому ответ можно записать таким образом:
х=π/6 + 2πn, n∈Z. Z - множество целых числе, т.е. n могут быть только целые числа: ..., -2, -1, 0, 1, 2, 3, ... .
В итоге получаем ответ: х=π/6 + 2πn, n∈Z.