Помогите, дали задачи по физике чтобы получить 4 за четверть Дам дополнительные баллы за...

Question

Помогите, дали задачи по физике чтобы получить 4 за четверть
Дам дополнительные баллы за правильное решение.
1 задача. Катер двигался вниз по течению реки. Зависимость его скорости V от времени t приведена на рисунке.
Сколько времени он плыл с выключенным мотором, если весь путь катер преодолел за время τ=10 мин со средней скоростью 2,2U, где U – скорость течения реки? Ответ выразить в мин, округлив до целых.
2 задача. На горизонтальном столе стоит цилиндрический сосуд с водой. В нём плавает кусок льда, привязанный нитью ко дну сосуда. Над поверхностью воды находится некоторый объём льда. Нить натянута с силой T=2 Н. На сколько изменится уровень воды в сосуде, если лёд растает? Ответ выразить в мм, округлив до целых. Если уровень понизится, то ответ следует внести со знаком «–». Площадь дна сосуда S=500 см2, плотность воды ρ=1 г/см3, ускорение свободного падения g=10 м/с2.

---

---

Answer 1

   В задачах на движение всегда участвуют три взаимосвязанные величины: S=V*t, где S - расстояние (пройденный путь), t - время движения и V - скорость. В случаях, когда рассматривается движение по течению, собственная скорость объекта V увеличивается на скорость течения U, и скорость объекта будет равна V+U.
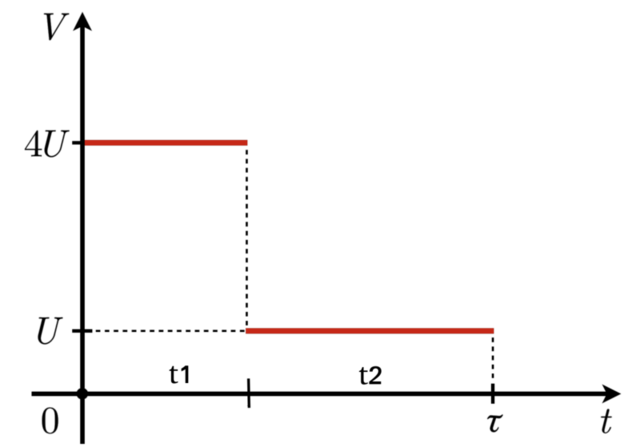
   Рассматриваемый катер прошел путь S за общее время τ = t1 + t2 = 10 мин, из которого t1 он двигался со скоростью 4U, а оставшееся время t2 — со скоростью течения реки U (см.рис).
   Из общей формулы можно получить систему:
S = 4U*(10 - t2) + U*t2;
S = 2,2U*τ = 2,2U*10 = 22U, и, решая систему, получаем
4U*(20 - t2) + U*t2 = 22U, сокращая на U, имеем 4*(10 - t2) + t2 = 22, откуда t2 = 6 мин

---