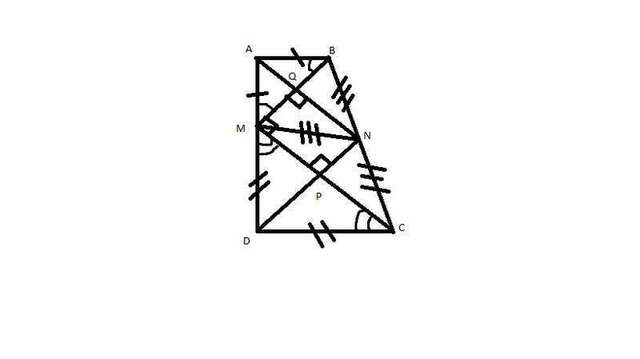
Имеем трапецию ABCD. По условию AB = AM и AD = AB + CD. Очевидно, AD = AM + MD. Приравняем эти равенства: AB + CD = AM + MD, и, поскольку, AM = AB, имеем: AB + CD = AВ + MD, вычтем из равенства AB и получим CD = MD. По условию, АВ перпендикулярна АD, угол MAB равен 90 градусов, и поскольку треугольник MAB равнобедренный, угол АМВ равен углу АВМ = (180 - 90)/2 = 45 градусов. Аналогично с треугольником MDC: поскольку AB параллельна CD, угол MDC равен 90 градусов. Угол DMC равен углу DCM = (180 - 90)/2 = 45 градусов. Угол АМD - смежный, равен 180 градусов по определению. Из этого имеем: угол BMС = 180 - угол АМВ - угол DMC = 180 - 45 - 45 = 90 градусов. Следовательно, треугольник BMC - прямоугольный.
Соединим точки M и N. Полученный отрезок MN = BN = NC, так как если описать окружность вокруг треугольника BMC, центром которой будет точка N, MN, BN и CN будут радиусами этой окружности. Рассмотрим треугольники ABN и AMN: угол ABM равен углу AMB, потому что треугольник равнобедренный, углы NBM и NMB равны аналогично. Из этого выходит, что треугольники ABN и AMN равны по двум сторонам и углу между ними. Треугольники BQN и MQN равны также по двум сторонам и углу между ними (BN = MN, QN - общая сторона, угол BNQ = углу MNQ). Углы NQB и NQM равны, и они - смежные; угол NQB = углу NQM = 180/2 = 90 градусов. Углы BMC и CMN равны 90 градусов. Далее, треугольники MNC и MDC равны по трем сторонам (MN = CN, MD = CD, DN - общая сторона). Треугольники MNP и CNP равны по двум сторонам и углу между ними (MN = CN, NP - общая сторона, угол MNP = углу CNP). Поскольку углы MPN и CPN равны и они смежные, то угол MPN = углу CPN = 180/2 = 90 градусов. Сумма углов четырех угольника равна 360 градусов. Угол QNP = угол NQM - угол QMP - угол MPN = 360 - 90 - 90 - 90 = 90 градусов, хоть для прямоугольника достаточно, чтобы хотя бы три угла были прямыми. Углы NQM, QMP, MPQ и PNQ равны 90 градусов. MPNQ - прямоугольник.