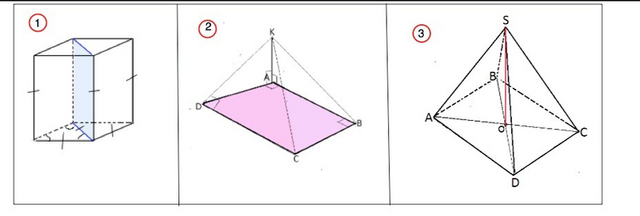
Задача 1.
Основание прямой призмы - ромб со стороной 5 см. и тупым углом 120°
. Боковая поверхность призмы имеет площадь 240 см².
Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
-------------
Ребра прямой призмы перпендикулярны плоскости оснований, следовательно, перпендикулярны сторонам и диагоналям оснований.⇒
Диагональное сечение является прямоугольником.
Сумма углов четырехугольника 360°.
Острый угол ромба равен (360°-2•120°):2=60°
Диагональ ромба делит его на два равных равнобедренных треугольника. Если угол при вершине такого треугольника 60°, – этот треугольник равносторонний. Поэтому меньшая диагональ ромба равна его стороне - 5 см.
Площадь боковой поверхности данной призмы - сумма площадей четырех равных прямоугольников.
Площадь каждого - 240:4=60 см²
Стороны диагонального сечения равны сторонам боковых граней. Сечение равно боковой грани.
Следовательно, его площадь равна площади боковой грани - 60 см²
-----------------------------------------------
Задача 2.
Через вершину A прямоугольника ABCD проведена прямая AK, перпендикулярная к плоскости прямоугольника.
Известно, что KD = 6 см, KB = 7 см, KC = 9 см.
Найдите расстояние от точки K до плоскости прямоугольника ABCD.
Сделаем рисунок.
Искомое расстояние - это длина отрезка ( перпендикуляра) КA.
КD ⊥ DC, так как проекция наклонной КD⊥ DC
Из прямоугольного треугольника КDС по теореме Пифагора найдем длину стороны DC прямоугольника АВСD
DC²=45
DC=АВ
АК=√(КВ²- АВ²)=√(49-45)=√4=2
--------------------------------
Задача 3.
Основание пирамиды - прямоугольник со сторонами 12 см и 16 см.
Все боковые рёбра пирамиды равны 26 см.
1) Докажите, что высота пирамиды проходит через точку пересечения диагоналей основания.
2) Найдите высоту пирамиды.
1)
Сделаем рисунок.
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
Так как все боковые ребра пирамиды равны между собой, их проекции на плоскость основания также равны между собой и соединяются в точке О пересечения диагоналей АС и ВD основания пирамиды. ⇒
Вершина пирамиды проецируется в точку пересечения диагоналей основания.
2)
Высоту пирамиды найдем из любого треугольника, образованного высотой пирамиды, половиной ее диагонали и боковым ребром.
Пусть это будет треугольник АSO.
SO²=AS²-AO²
АО - половина диагонали прямоугольника АВСD.
По теореме Пифагора из прямоугольного треугольника АВС
АО=1/2√(АВ²+ВС²) =1/2√(144+256)=10 см
SO²=26²-10²=676-100
SO=√576=24 см
Ответ: Высота пирамиды равна 24 см