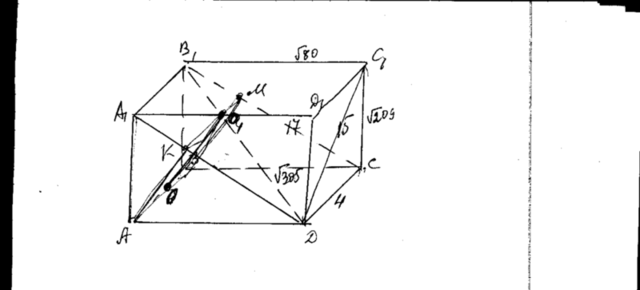
Для построения общего перпендикуляра скрещивающихся прямых АВ и В1D проведем плоскость через DB1 параллельно АВ. Это будет плоскость DСВ1А1, т.к. АВ||А1В1.
Теперь проектируем прямую АВ на эту плоскость. АК⊥А1D, ВМ⊥В1С. Проекция получается КМ. ИЗ точки О1, где пересеклись КМ и В1D, проводим О1О параллельно АК. О1О= и будет общим перпендикуляром для скрещивающихся прямых.
О1О=АК. СС1=√((DC1)²-DC²)=√209.
B1C=√(B1D²-DC²)=√(289=17
B1C1=√(B1C²-C1C²)=√80
Из ΔААD найдем АК=АА1*АD/A1D=√209*√80/17=4√1045/17.