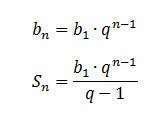Геометрическая прогрессия
a) b(10)=1*3^(10-1)=3^9=19683
S(10)=19683/(3-1)=9841.5
b) так как b(8)=2, и b(8)=b(1)*q^7=2 ( по определению) решаем полученное уравнение
b(1)*0.5^7=2
b(1)=2^8=256
S(8)=(256*0.5^7)/(0.5-1)=2/(-0.5)=-4
в) так как известно b(7)=1458, запишем по определению
b(7)=b(1)*q^6
1458=2*q^6
729=q^6
q=3
S(7)=(2*729)/(3-1)=729
для удобства в скобках записал номера членов прогрессии, чтобы не перепутать, т.е. S(7) - это сумма семи членов прогрессии, b(5) - это пятый член прогрессии, думаю, понятно, формулы по которым все высчитывается - во вложении