Помогите пожалуйста!И не надо просто в и-нете ответы искать! 1)диаметр окружности...

Question

Помогите пожалуйста!И не надо просто в и-нете ответы искать!
1)диаметр окружности описанной около прямоугольного треугольника равен 13,а расстояние от центра окружности до одного из катетов равно 2,5.Найдите площадь треугольника.
2)Дан правильный шестиугольник ABCDEF со стороной,равной 4.Найти радиус окружности вписанной в треугольник ACE.

Answer 1

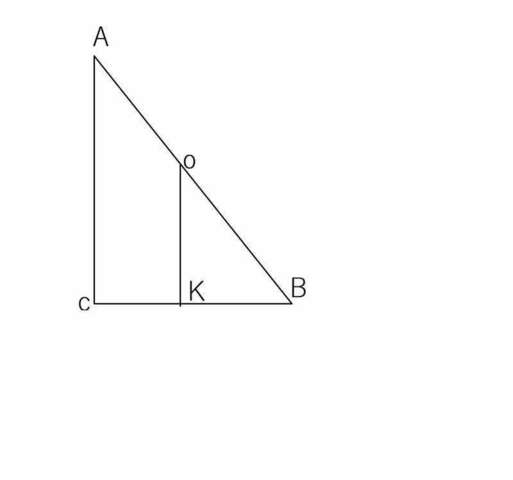
Центр описанной окружности - середина гипотенузы. ⇒ OK=2,5
                                                                                     AB=13
ΔACB подобен ΔВОК (∠ B - общий, ∠BCA=∠OKB=90°)
AB/OB=AC/OK=2/1
Откуда AC=2 OK=5
По теореме Пифагора BC=√(169-25)=12
S=BC· AC=12·2/2=12
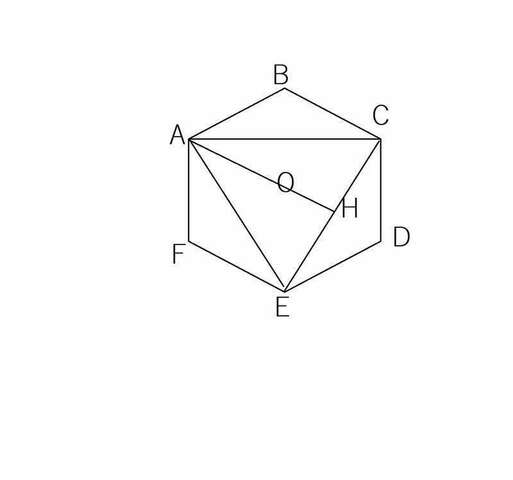
2) ∠BAC=BCA=∠FAE=(180-120)/2=30°
⇒∠EAC=ACE=∠CEA=60°
OH=1/3AH, ГДЕ AH-высота,
AC²=AB²+BC²-2AB·BC cos 120°=16+16+16=48
AH=√(AC²-Ch²)=√(AC²-AC²/4)=√36=6
OH=6/3=2

---

---