Через образующую цилиндра проведены две плоскости. Это значит, что
образующая цилиндра является линией их пересечения.
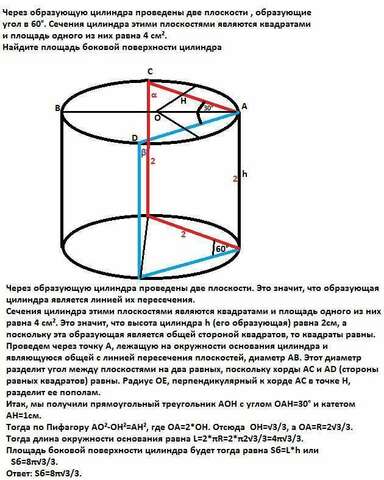
Сечения цилиндра этими плоскостями являются квадратами и площадь одного из них равна 4 см². Это значит, что высота цилиндра h (его образующая) равна 2см, а поскольку эта образующая является общей стороной квадратов, то квадраты равны.
Проведем через точку А, лежащую на окружности основания цилиндра и являющуюся общей с линией пересечения плоскостей, диаметр АВ. Этот диаметр разделит угол между плоскостями на два равных, поскольку хорды АС и АD (стороны равных квадратов) равны.
Радиус ОЕ, перпендикулярный к хорде АС в точке Н, разделит ее пополам.
Итак, мы получили прямоугольный треугольник АОН с углом ОАН=30° и катетом АН=1см. Тогда по Пифагору АО²-ОН²=АН², где ОА=2*ОН.
Отсюда ОН=√3/3, а ОА=R=2√3/3.
Тогда длина окружности основания равна L=2*πR=2*π2√3/3=4π√3/3.
Площадь боковой поверхности цилиндра будет тогда равна Sб=L*h или Sб=8π√3/3.
Ответ: Sб=8π√3/3 ≈14,5 .