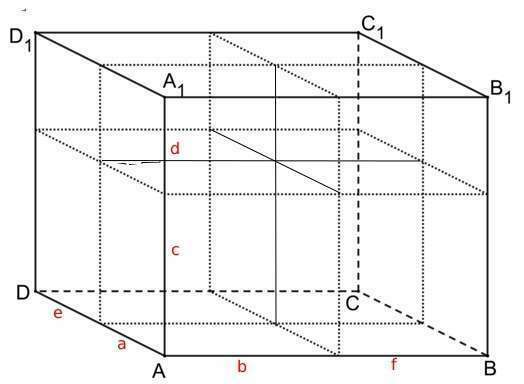
Начнём
с того, что площади поверхностей брусков,
очевидно, могут быть вычислены по общей
формуле для определения полной поверхности
прямоугольных параллелепипедов, Sпп =
2(аb + bc + ac), где a, b, с — длины рёбер брусков.
Обозначим
полные площади поверхностей брусков,
привязав их к соответствующим вершинам,
как
SА, SВ, SС, SD, SA_1, SB_1, SC_1, SD_1. Введём также
обозначения для длин рёбер брусков
a,
b, c, d, e, f (см. рис.).
Тогда для каждого из
брусков можем записать рёбра:
SА
— a, b, c; SA_1 — a, b, d;
SВ
— a, f, c; SB_1 — a, f, d;
SС
— e, f, c; SC_1 — e, f, d;
SD
— e, b, c; SD_1 — e, b, d;
Внимательно
рассмотрев соотношения для площадей
полных поверхностей брусков исходя из
принятых обозначений, можно заметить,
что
SA
+ SB_1 +
SC
+ SD_1 = SA_1 + SB +
SC_1
+ SD, откуда
SC_1
=
SA
+ SB_1 +
SC
+ SD_1 - SA_1 - SB - SD.
Подставляя
исходные
данные в выведенную формулу, получаем
SC_1
=
78
+ 62
+
72
+ 170
- 110
- 42 - 126
= 104