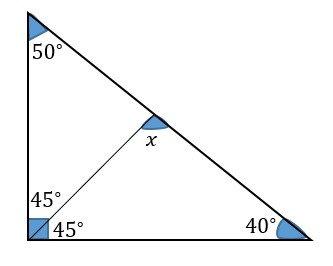
Оба рисунка во вложении.
Биссектриса проведенная из прямого угла на гипотенузу, делит прямой угол на два равных угла, равные -

.
Поначалу найдем второй острый угол:
Зная что у прямоугольного треугольника, сумма острых углов равна

, то получаем:
 Теперь следуем порядку рисунков во вложении:
1. Следуя теореме о сумме углов треугольника, получаем:
Теперь следуем порядку рисунков во вложении:
1. Следуя теореме о сумме углов треугольника, получаем:

2. Следуя теореме о сумме углов треугольника, получаем:

В геометрии, угол между прямыми называется наименьший угол, между этими прямыми, следовательно - угол между биссектрисой прямого угла и гипотенузы равен 
.