Находим производную f'(x) = (x^4 - x²)' = 4x³ -2x = 2x(2x² -1).
Ищем критические точки, решая уравнение f'(x)=0.
2x(2x²-1) = 0
2x=0, 2x²-1 = 0
x=0, x=1/√2, x= -1/√2. Это критические точки.
________ -1/√2________0_______1/√2________
- + - +
убыв. возр. убыв. возрастает.
Теперь вычисляем значения у в точках экстремумов
у√(-1/√2)= (-1/√2)^4 - (-1/√2)² = 1/4 -1/2 = - 1/4.
y(0) = 0
y(1/√2) = -1/4. функция четная.
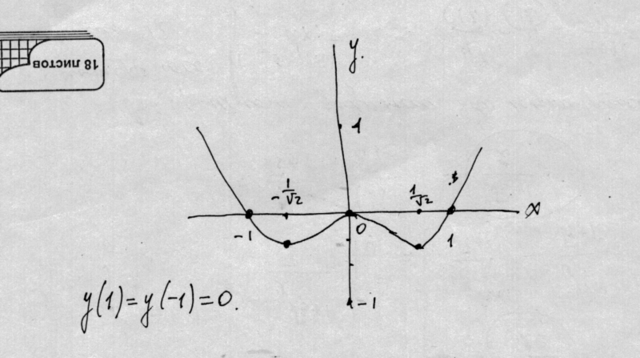
Наносим точки и строим график.Считаем дополнительные точки при 1,-1,2,-2.