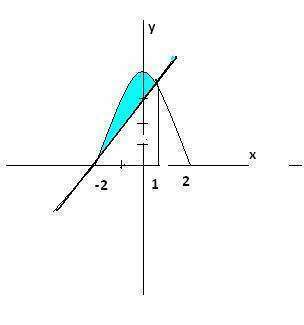
Находим точки пересечения этих кривых:
x+2=4-x²
-x²-x-2=0
Решаем кв. уравнение
x₁=-2 x₂=1
Ищем первообразную от первой кривой:
y=4-x² F(x)=4x-x³/3+c
Находим первообразные в точках -2 и 1
F(-2)=-8+8/3=-16/3
F(1)=4-1/3=11/3
11/3+16/3=27/3=9
Значение функции в точках -2 и 1
y=4-(-2)²=0
y=4-1²=3
или
y=-2+2=0
y=1+2=3
Тоже самое, потому что это точки пересечения графиков.
Площадь треугольника под графиком функции y=2+x
0.5*(1+2)*(3-0)=3
Площадь фигуры пересечения
9-3=6
Рисунок во вложении