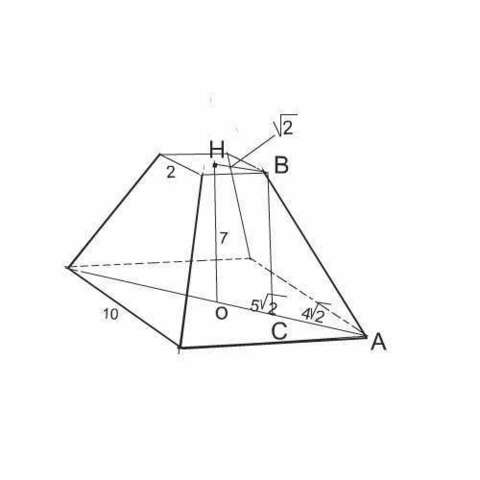
Сделаем рисунок к задаче.
Проведем в каждом основании диагонали.
По формуле диагонали квадрата ( а, так как пирамида правильная, основания в ней - квадраты)
d=а√2, а половина диагонали равна а√2):2,
ОА=10√2):2=5√2
НВ= 2√2):2=√2
Рассмотрим прямоугольную трапецию ОНВА
Ее высота =7 см
Основания -
меньшее √2 см
большее - 5√2 см
Опустим из В к основанию ОА перпендикуляр.
Получим прямоугольный треугольник АВС, катет которого АС = разности оснований:
АС=АО-ВН=5√2-√2=4√2
ВС=НО=7 см
Теперь самое время вспомнить о теореме Пифагора.
АВ=√(ВС²+АС²)=√81=9 см