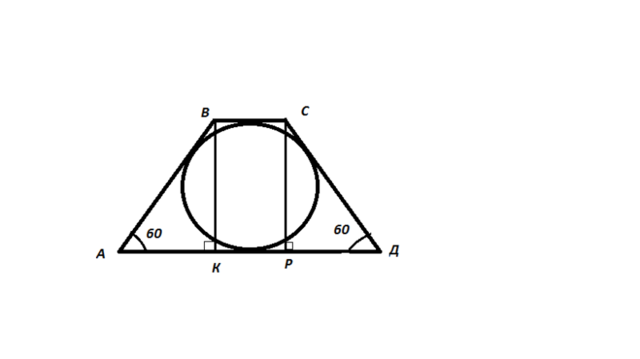Т к по условию угол СВА=ВСД=120 градусов, то угол А=Д=180-120=60градусов.
Проведем высоту ВК и получим прямоугольный треугольник АВК. Рассмотри его. Угол АВК=180-(60+90)=30 градусов => АК=1/2АВ, тогда пусть АК=х. Если провести вторую высоту из угла С, то отрезки АК=КР=РД=х (т е АД=3х), а АВ=СД=2х. ВС=КР=х.
Sтрапеции=1/2(ВС+АД)*ВК.
В равнобедренной трапеции квадрат высоты равен произведению ее оснований т е ВК=корень из ВС*АД. Подставим значение в формулу площади:
S=1/2(ВС+АД)*корень из ВС*АД=1/2*(х+3х)*корень из х*3х=2х*хкорней из 3;
Из этого уравнение выражаем 2х^2=98корней из3/корень из 3; х=7(см)-ВС, тогда АД=3х=21(см).
Средняя линия трапеции равна полусумме длин ее оснований: Ср л=1/2(ВС+АД)=1/2*28=14(см).
ОТВЕТ:14см.