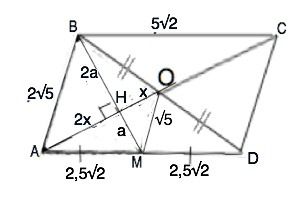
ABCD- параллелограмм. Диагонали параллелограмма при пересечении делятся пополам.
В треугольнике AВD:
ВО=OD⇒ AO - медиана.
AM=DM( дано)⇒
BM- медиана.
Н- точка пересечения медиан, ∠AHВ=90°( дано)
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
Примем MН=а, тогда BH=2a
Примем ОН=х, тогда AН=2х
–––––––––
Из прямоугольного ∆ ABН по т.Пифагора
AН²=AB²-BH²
4х²=(2√5)²-(2a)²
Из прямоугольного ∆ AHM по т.Пифагора
AН²=AM²-MH²
4x²=(2,5√2)²-a²
Приравняем значения 4х² из двух уравнений:
20-4a²=12,5-a²
3a²=7,5
a²=2,5
Из ∆ АВН по т.Пифагора
АН²=АВ²-ВН²
4х²=20-4а²=20-10
х²=2,5
Из ∆ ОВН по т.Пифагора
ВО²=ВН²+ОН²
ВО²=2,5+10=12,5
ВО=2,5√2
BD=2•BO=5√2 (ед. длины)