1)Дано: прямая МА перпендикулярна к плоскости треугольника АВС. Докажите, что МА перпендикулярна ВС.
–––––––––––––––––––––
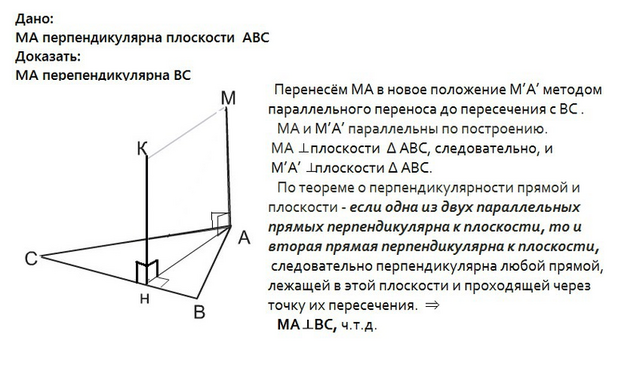
Сделаем рисунок, соответствующий условию.
Прямые МА и ВС не лежат в одной плоскости. следовательно, они скрещивающиеся. Угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым
Перенесём МА в новое положение М’А’ методом параллельного переноса до пересечения с ВС .
МА и М’А’ параллельны по построению. МА ⊥плоскости ∆ АВС, следовательно, М’А’ ⊥ плоскости ∆ АВС. По теореме о перпендикулярности прямой и плоскости - если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к плоскости, следовательно перпендикулярна любой прямой, лежащей в этой плоскости и проходящей через точку их пересечения. ⇒
МА⊥ВС, ч.т.д.
–––––––––––––––––
2)Четырёхугольник АВСД = квадрат, точка О - его центр. Прямая ОМ перпендикулярна к плоскости квадрата.
а) Докажите, что МА=МВ=МС=МД.
б) Найдите МА. если АВ=4 см, ОМ=1 см.
______
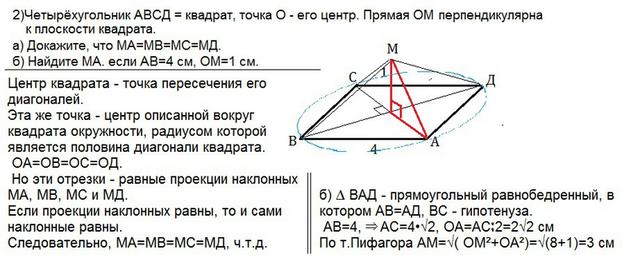
а)См. рисунок во втором приложении.
Центр квадрата - точка пересечения его диагоналей. Эта же точка - центр описанной вокруг квадрата окружности, радиусом которой является половина диагонали квадрата.
Радиусы ОА=ОВ=ОС=ОД. Но эти отрезки - равные проекции наклонных МА, МВ, МС и МД. Если проекции наклонных равны, то и сами наклонные равны. Следовательно, МА=МВ=МС=МД, ч.т.д.
б) ∆ ВАД - прямоугольный равнобедренный, в котором АВ=АД, ВС - гипотенуза.
АВ=4, ⇒ АС=4•√2, ОА=АС:2=2√2 см
По т.Пифагора АМ=√( ОМ²+ОА²)=√(8+1)=3 см