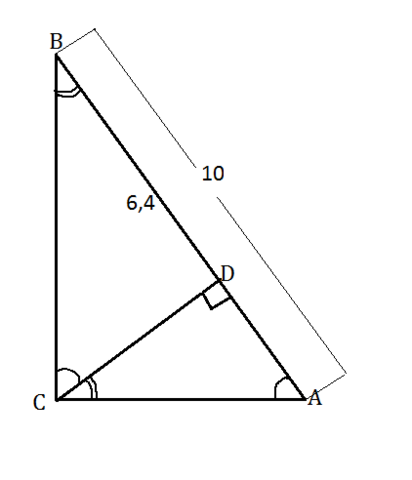
Найдем AD10-6,4=3,6
Высота прямоугольного треугольника, проведенная к гипотенузе, делит треугольник на подобные треугольники.
Из подобия ∆ ABC и ∆ ADC следует отношение:
АВ:АС=АС:AD ⇒
AC²=AB*AD=10*3,6=36
AC=√36=6
Из подобия ∆ ABC и ∆ ВDC следует отношение:
АВ:ВС=ВС:BD ⇒
BC²=AB*BD=64
BC=8
Из подобия ∆ BCD и ∆ ACD следует отношение: ВD:CD=CD:AD
CD²=AB*CD=6,4*3,6=23,04
CD=√23,04=4,8
Отсюда следует свойство высоты, которое полезно запомнить:
а) Высота прямоугольного треугольника, проведенная из прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.
----
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
-------
Тогда решение задачи можно записать короче:
CD²=AB*CD=6,4*3,6=23,04
CD=√23,04=4,8 см
BC²=AB*BD=64
BD=√64=8 см
AC²=AB*AD=10*3,6=36
AC=√36=6 см