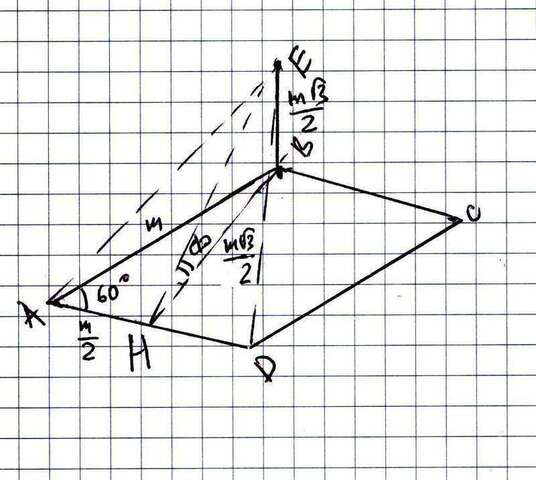
В плоскости АВС проведем высоту ромба ВН, перпендикулярно AD, точки Е
и Н соединим, прямая ЕН лежит в плоскости АED, и она перпендикулярна AD
по построению - AD перпендикулярно любой прямой в плоскости EНB, потому
что в этой плоскости есть 2 прямые, ей перпендикулярные - BН и EB.
Поэтому угол ЕНВ = Ф - угол между плоскостями АСВ и АЕD.
Далее, ВН = АВ*sin(60) = m*корень(3)/2; и мы видим, что прямоугольный
треугольник ЕВН - равнобедренный, ЕВ = ВН. А Ф в нем - острый угол.
Поэтому Ф = 45 градусов