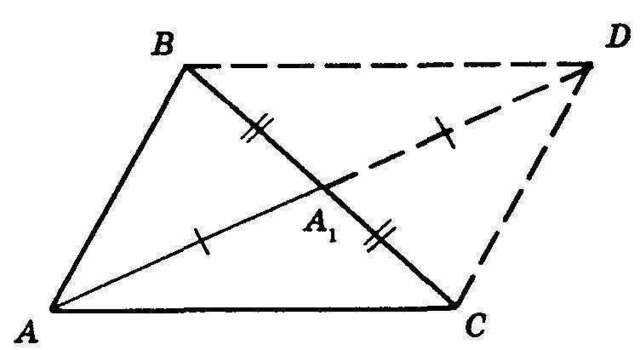
Пусть вмедианаНужно доказать, чтоПродолжим медианузаи на продолжении отложимТогда полученный четырехугольникбудет параллелограммом, так как его диагонали AD и ВС в точке пересечения делятся пополам, значит, BD = АС. К тому жеВсторона меньше суммы двух других сторон, то есть
Что и требовалось доказать