Най­ди­те p и по­строй­те гра­фик функ­ции y=x2+p если из­вест­но, что пря­мая y=-2x...

Question

Най­ди­те p и по­строй­те гра­фик функ­ции y=x2+p если из­вест­но, что пря­мая y=-2x имеет с гра­фи­ком ровно одну общую точку.

Answer 1

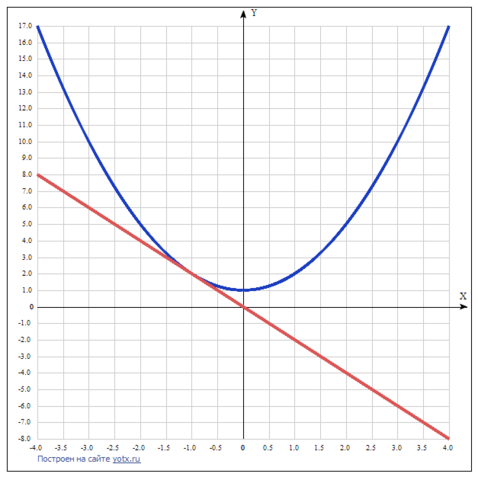
Если пря­мая y=-2x имеет с гра­фи­ком ровно одну общую точку, то производная функции равна -2:f'(x) = 2x.
Приравниваем: 2х = -2
                              х = -2 / 2 = -1.
                              у = -2х = -2*(-1) = 2.

Общая точка - это касательная к графику.
Координаты точки касания определены: (-1; 2).

Подставим эти координаты в уравнение функции:
2 =(-1)² + р.
Отсюда находим р = 2 - 1 = 1.

Ответ: уравнение функции имеет вид у = х² + 1.

График и таблица координат параболы для её построения даны в приложении.
Для построения прямой достаточно двух точек.
Задаём значения "х" и рассчитываем значение "у".
х  = 0,   у = 0,
 х = 3,   у = -2*3 = -6.     

---