Докажите равенство прямоугольных треугольников по катету и высоте, опущенной **...

Question

Докажите равенство прямоугольных треугольников по катету и высоте, опущенной на гипотенузу. Дайте пожалуйста полный ответ(можно с рисунком)

Answer 1

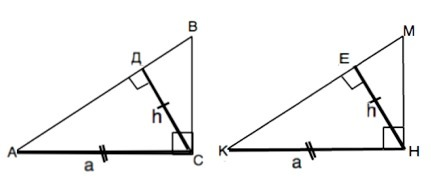
Обозначим треугольники АВС и КМН, в которых ∠С=∠Н=90°, катеты АС=КН и высоты СД=НЕ.

Примем длину равных катетов равной а, высот - равной h.

Синус ∠А=h/а, синус угла К=h/а ⇒ эти углы равны. 

Следовательно. ∆ АСВ=∆ КНМ по второму признаку равенства треугольников:  стороне АС=КН и двум углам С=Н и А=К .

---