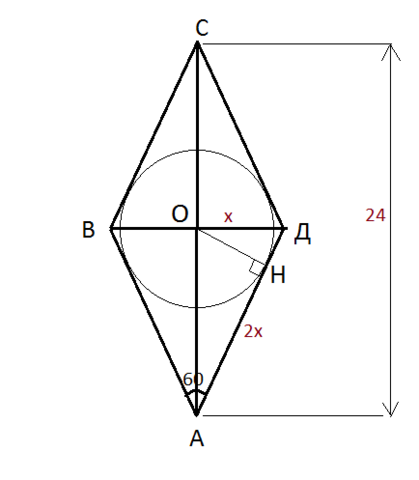
Диагонали ромба пересекаются под углом 90°
и диагонали ромба делят углы пополам ⇒
рассмотрим ΔАОД- прямоугольный
т.к. ∠А=60, то∠ОАД=60/2=30°
получили, что катет ОД лежит против угла 30° ⇒
он а 2 раза меньше гипотенузы
пусть ОД=х
тогда АД=2х
АО=24/2=12 (т.к. диагонали ромба точкой пересечения делятся пополам)
по теореме Пифагора:
х²+12²=(2х)²
х²+144-4х²=0
-3х²+144=0
3х²-144=0
3х²=144
х²=144/3=48
х=√48=4√3 сторона ОД
тогда ВД=4√3*2=8√3
АД=8√3
r=(d1*d2)/4а=(24*8√3)/(4*8√3)=24/4=6
длина окружности l=2*π*r=2*6*π=12π