Формула площади ромба через диагонали:
S=(d1*d2)/2
d1 и d2 диагонали ⇒
S=336, d1=14
336=(14*d2)/2 решаем...
14*d1=336*2
14*d1==672
d1=672/14=48 - вторая диагональ
2 способ:
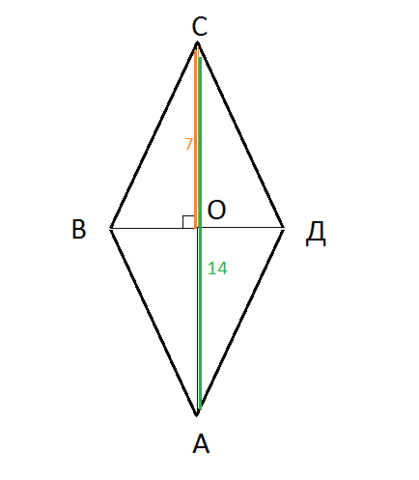
ромб АВСД
О - точка пересечения диагоналей
Пусть диагональ СА=14
тогда СО=14/2=7 (т.к. диагонали точкой пересечения делятся пополам)
S(АВСД)=336
а диагонали ромба разбивают его на 4 равных треугольника ⇒ площадь одного треугольника =360/4=84см²
рассмотрим ΔВОС -прямоугольный (т.к. диагонали ромба пересекаются под прямым углом)
S(ВОС)=(ВО*ОС)/2
S(ВОС)=84
СО=7 подставляем
84=(7*ВО)/2
7*ВО=168
ВО=24 - это половина нашей диагонали ВД ⇒
ВД=24*2=48