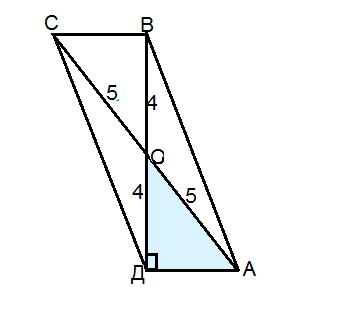
Площадь параллелограмма находят произведением его высоты на сторону, к которой она проведена.
Пусть данный параллелограмм АВСД.
Тогда ВД ⊥ АД, является поэтому его высотой и равна 8 см.
Диагонали параллелограмма точкой из пересечения делятся пополам.
Треугольник АОД - прямоугольный, гипотенуза АО=5 см, катет ОД=4 см.
По т. Пифагора АД=3 см ( это следует и из того, что треугольник из отношения его сторон "египетский" и второй катет равен 3 см)
S=ВД*АД=8*3=24 см²