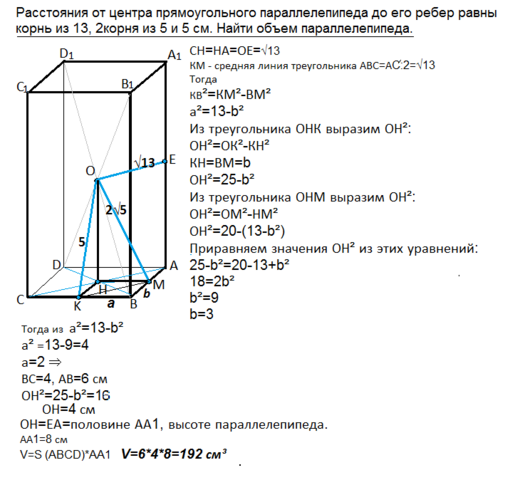
Пусть дан параллелепипед АВСDA₁B₁C₁D₁
Все его грани - прямоугольники.
Центр - точка О пересечения диагоналей этого параллелепипеда. . Расстоянием от О до ребер параллелепипеда являются перпендикуляры к ним из О, причем, т.к. О - центр параллелепипеда, то перпендикуляры к ребрам будут пересекаться с ними в их середине.
ОЕ =√13=расстояние от О до АА1
ОМ =2√5- расстояние от О до АВ
ОК=5- расстояние от О до ВС
АЕ=ЕА₁
АМ=ВМ
ВК=КС
Диагонали основания АВСД равны и пересекаются в точке Н,
ОН⊥ плоскости АВСД
СН=НА=ОЕ=√13
КМ - средняя линия треугольника АВС=АC:2=√13
Тогда КВ²=КМ²-ВМ²
а²=13-b²
Из треугольника ОНК выразим ОН²:
ОН²=ОК²-КН²
КН=ВМ=b
ОН²=25-b²
Из треугольника ОНМ выразим ОН²:
ОН²=ОМ²-НМ²
ОН²=20-(13-b²)
Приравняем значения ОН² из этих уравнений:
25-b²=20-13+b²
18=2b²
b²=9
b=3
Тогда из а²=13-b²
а²=13-9=4
а=2⇒
ВС=4,
АВ=6
ОН²=25-b²=16
ОН=4
ОН=ЕА=половине АА₁, высоте параллелепипеда.
АА₁=8
V=S (ABCD)*AA₁
V=6*4*8=192 см³