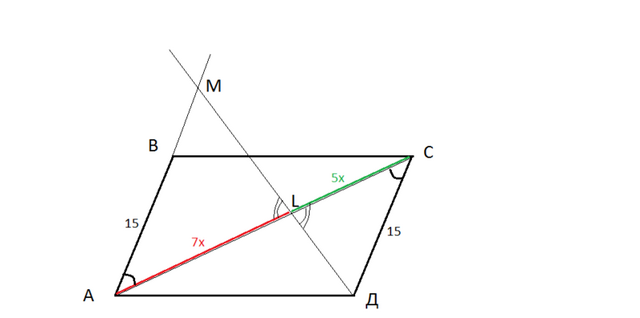
ΔАМL подобен ΔСДL (по двум углам: ∠АLМ=∠СLД как вертикальные, ∠МАL=∠ДСL как внутренние накрест лежащие при прямых АВ||СД и секущей АС)
сторона АВ=СД (т.к. у параллелограмма противолежащие стороны равны)
СД/АМ=5/7
15/АМ=5/7
АМ=(15*7)/5=21
ВМ=АМ-АВ=21-15=6
ΔАМL подобен ΔСДL (доказывалось ранее)
LС/LА=5/7 - коэффициент подобия
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. ⇒
S(СДL)/S(АМL)=(5/7)²=25/49