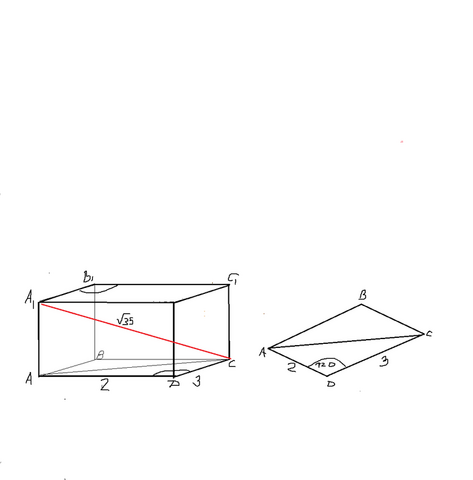
Для решения задачи необходимо найти высоту параллелограмма.
Высоту АА1 найдем пз прямоугольного треугольника АСА1
АА1=√(А1С²-АС²)
АС² найдем по теореме косинусов:
АС²=АD²+DC²- 2*AD*DC*cos(120°)
АС²=4+9-12 (-0,5) =19
АА1=√(35-19)=√16=4
Площадь боковой поверхности прямого параллелепипеда равна произведению его высоты на периметр основания.
Sбок=4*2(2+3)=40 см²
Площадь основания равна произведению сторон параллелограмма на синус угла между ними.
S осн=2*3*sin(120°)=6*√3):2=3√3
Полная площадь равна сумме площадей боковой поверхности и двух оснований параллелепипеда.
S полн=40 см²+2*3√3 или 40см²+10,392см²=50,392 см²