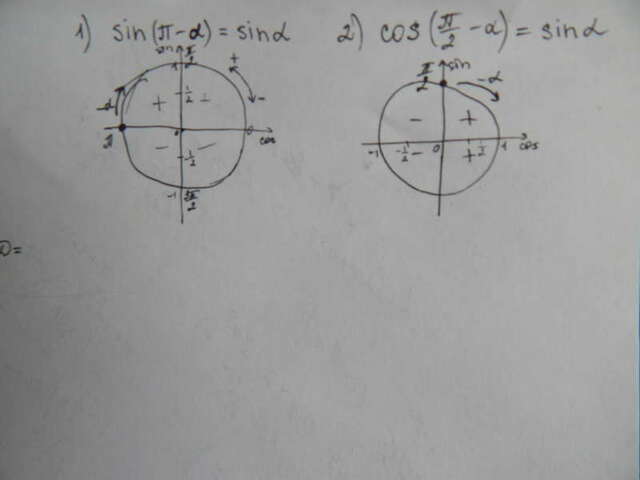Объясню преобразование каждого множителя по порядку:
1) sin(п-а) преобразуем по формулам приведения.
Если прибавляется 180° или п (2п, 3п и т.д.), тригонометрическая функция
остаётся та же. Что же касается знака «-» перед а – он вычисляется по
окружности.
У синуса значения положительные в 2-х верхних четвертях и отрицательные в
нижних. Отмечаем нашу точку П, и ведём пальцем в стороны уменьшения по
окружности (вправо), как будто мы вычитаем эту самую а. Смотрим: какой знак у sin в
этой четверти, так знак и оставляем.
Получается sin а.
2) Если прибавляется 90° или п/2 (3п/2, 5п/2 и т.д.), функция меняется на
противоположную (sin на cos, cos на sin, tg на ctg и наоборот). Теперь смотрим
на окружность: отмечаем П/2 и ведём опять же в сторону уменьшения, вправо, т.к.
у нас –а (если бы было +а, для определения знака нужно было бы вести в сторону
увеличения – влево). Смотрим, какой знак у косинуса в данной плоскости (а у
косинуса положительный в правых четвертях и отрицательные в левых).
Исходя из всего вышесказанного, cos(п/2
–а) = sin а.
3) cos2а
– это формула двойного угла. Её можно записать в 3-х видах (2 последние
выводятся из первой):
cos(2a) = cos^2(a)
– sin^2(a)
cos(2a) = 1 – 2sin^2(a)
cos(2a) = 2cos^2(a) –
1
Думаю, в нашем случае больше подойдёт вторая формула.
Итак. Вот что у нас получилось:
Sin(п-а)*cos(п/2 –а)+cos2а = sin(a)*sin(a)+(1-2sin^2(a))
= sin^2(a) +1 – 2sin^2(a) = 1 – sin^2(a) = cos^2(a)
[Исходя из
основной тригонометрической формулы sin^2(a) + cos^2(a) = 1]