В правильный шестиугольник вписана окружность радиуса r. Найдите площадь шестиугольника.

0 голосов
432 просмотров

В правильный шестиугольник вписана окружность радиуса r. Найдите площадь шестиугольника.

Геометрия (29 баллов) | 432 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

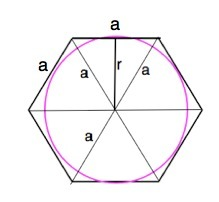
Площадь описанного многоугольника равна произведению его полупериметра на радиус вписанной окружности. 

S=p•r

Стороны правильного шестиугольника равны радиусу описанной около него окружности, т.е. стороне  a правильного треугольника с высотой, равной радиусу r вписанной окружности. 

Периметр P шестиугольника 6a, полупериметр p=3a. 

a= \frac{r}{sin60^o} = \frac{2r}{ \sqrt{3} }

p= \frac{6r}{ \sqrt{3} }

S= \frac{r*6r}{ \sqrt{3} } = \frac{6 r^{2} \sqrt{3} }{ \sqrt{3}* \sqrt{3} } =2 r^{2} } \sqrt{3}

image
(228k баллов)
Похожие задачи