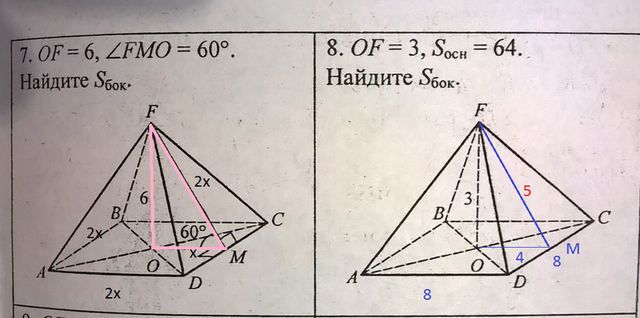
В основании пирамиды квадрат АВСД
FM=L- апофема боковой грани.
S(бок.)=Р(осн.)·L/2
Рассматриваем прямоугольный треугольник FOM
Один угол 60°, значит второй острыйугол 30°.
Катет, лежащий против угла в 30°, равен половине гипотенузы
Пусть FM=2x, тогда ОМ=х
По теореме Пифагора
FO²=FM²-OM²
6²=(2x)²-x²
36=3x²
x²=12
x=2√3
2x=4√3
АВ=ВС=СD=AD=4√3
L=FM=4√3
S(бок.)=Р(осн.)·L/2=16√3·4√3/2=96 кв ед.
8.
В основании пирамиды квадрат АВСД
АВ=ВС=СD=AD=а
S(осн.)=а²
а²=64
а=8
Рассматриваем прямоугольный треугольник FOM
FО=3,
ОМ=а/2=4
По теореме Пифагора
FM²=FO²+OM²=3²+4²=9+16=25
FM=5
S(бок.)=Р(осн.)·L/2=4·8·5/2=80 кв ед.