1. a)√900 = 30
0,3*30=9
б)√(0,64*49)= √0,64 * √49 = 0,8*7=5,6
в)√(3 ⁴ * 2 ⁶)= √ 3⁴ * √2⁶ = 3² * 2³ = 9*8 = 72
г)√40*√10 - √20/√5 = √(40*10) - √(20/5) =√400 - √4 = 20-2 =18
2. Если маленькая сверху - это квадрат, то в таком случае:
а)4x²-20=0
4х² = 20
х² = 20/5
х² = 4
х=+2; -2
б)3х²+5х=0
х выносим за скобку
х(3х+5)=0
х = 0 3х+5=0
3х= -5
х = -(5/3)
в)х²-5х-24=0
тут можно решить либо через дискриминант, либо по теореме Виета
1) через дискриминант:
х²-5х-24=0
D= (-5)² -( -24)*4 = 25+96 = 121 √121=11
х₁ = (-(-5) + 11) / 2 = (5+11)/2= 16/2 =8
х₂ = (-(-5)-11)/2 = (5-11) /2= -6/2= -3
2) по теореме Виета:
х₁+х₂ = -(-5)= 5
х₁*х₂= -24
х₁= 8 х₂ = -3
4.Разложите на множители
х²-5х-24=0
(х+3)(х-8)=0
х² -8х+3х -24 = 0 ( решение можно посмотреть выше, во втором задании под буквой "в")
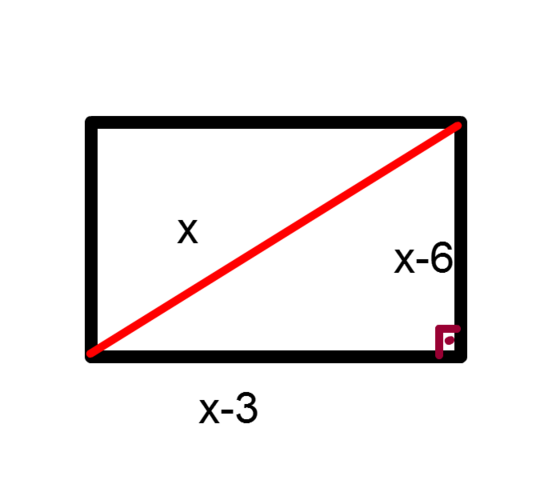
3.
Диагональная прямая на 6 см больше одной из сторон и на 3 см больше другой. Найдите стороны прямоугольника
(х-3)² +(х-6)² = х²
х²-6х+9 + х² -12х + 36 = х²
х² - 18х + 45 =0
1) по теореме Виета
х₁+х₂= - (-18) = 18
х₁*х₂ = 45
х₁= 15 х₂ = 3
2) через дискриминант
D= 324-180=144 √144 =12
х₁ = (-(-18) + 12) / 2 = (18+12)/2= 30/2 =15
х₂ = (-(-18)-12)/2 = (18-12) /2= 6/2= 3
......
......
х = 15, тк в задаче говорилось, что одна из сторон меньше диагонали( то, что мы за х обозначили) на 3 см, а другая на 6, а 3-3=0, такого быть не может
если диагональ равна 15, то стороны соответственно будут равны
х-6=15-6=9 см
х-3=15-3=12 см