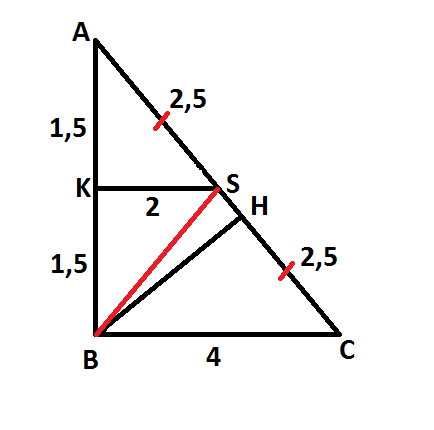В правильной четырёхугольной пирамиде, апофемой называется высота боковой грани.
В данной задаче нужно найти расстояние от центра основания пирамиды до боковой грани. Под расстоянием до боковой грани, понимается расстояние до центра боковой грани, данный центр находится в центре апофемы.
Центр апофемы делит её пополам (5/2=2,5).
Построим треугольник АВС:
АВ - высота пирамиды равная 3
АС - апофема равная 5
ВС - расстояние до ребра грани, так как треугольник АВС прямоугольный (следует из того что АВ - высота), то по теореме Пифагора ВС=4 (25=9+16).
BH - является высотой треугольника ABC
BS - является медианой ABC, (AS=SC=2,5)
Опустим перпендикуляр из точки S на высоту пирамиды AB, образуем точку K. Треугольник AKS является прямоугольным и подобным треугольнику ABC, (стороны треугольника AKS относятся у сторонам треугольника ABC в отношении 1/2, то есть треугольник AKS в два раза меньше треугольника ABC). AK=KB=1,5; треугольник BKS прямоугольный и он равен треугольнику AKS значит BS=2,5.
Ответ: 2,5