Задачу можно решить методом «научного тыка»
Допустим, в какой-то момент малыш Федя обгоняет Женю. Отметим это место специальной меткой, как условное начало круга. Как только он обгоняет Женю, он понимает, что (теперь уже) она – впереди него на расстоянии длины круговой дорожки (фактически она почти впритык позади него, но ведь дорожка круговая (!), а значит, Женя, как бы и впереди на расстоянии длины дорожки).
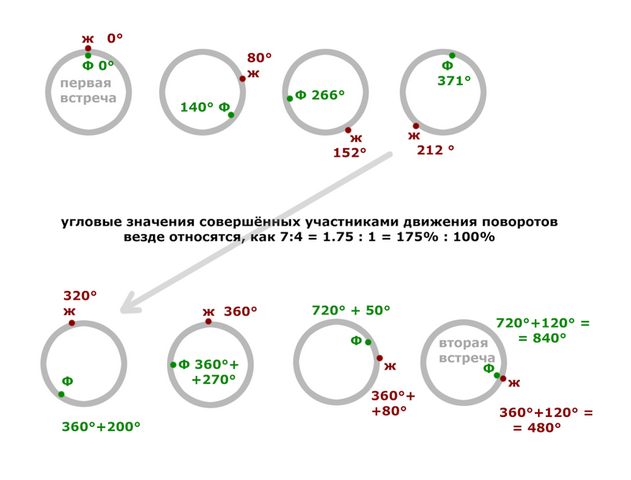
Пускай Женя пройдёт после первой встречи целый круг. Для того, чтобы Феде догнать Женю, ему нужно проехать всю круговую дорожку до того места, где в прошлый раз была Женя (т.е. целый круг) и ещё один круг, чтобы уже и догнать Женю второй раз. Но для этого ему нужно было бы ехать вдвое быстрее, т.е. на 100% быстрее, а он едет только на 75% быстрее. Значит, до второй встречи Женя успеет пройти больше, чем один круг.
Итак, учитывая это, пускай теперь до нового места встречи Женя пройдёт целый круг от метки до метки, и ещё дополнительно от метки какую-то часть круговой дорожки, назовём это «кусок дорожки», а малыш Федя до этого нового места встречи проедет на велосипеде целых два круга и ещё такую же часть дорожки, как и Женя, т.е. такой же «кусок».
Новое место встречи, таким образом, сместилось от начальной метки на «кусок дорожки».
После второй встречи, Федя опять обгонит Женю и потом опять встретится с ней уже в третий раз со смещением ещё на один «кусок дорожки» от предыдущего места встречи, которое и так уже было смещено от начальной метки на «кусок дорожки», стало быть, третья встреча сместится от начальной метки на «два куска дорожки».
До второго места встречи Женя прошла
круг и ещё «кусок дорожки»,
а Федя проехал два круга и «кусок дорожки».
До третьего места встречи Женя прошла
2 круга и ещё «два куска дорожки»,
а Федя проехал четыре круга и ещё «два куска дорожки».
До четвёртого места встречи Женя прошла
3 круга и ещё «три куска дорожки»,
а Федя проехал шесть кругов и ещё «три куска дорожки».
Заметим, что если бы Женя к четвёртому месту встречи, смещённому от начальной метки на «три куска дорожки», прошла бы 4 целые круга (три плюс один), то тогда Федя проехал бы 6 кругов и ещё «три куска дорожки», т.е. такое же расстояние, как и Женя, а значит ещё один добавочный круг, и всего – семь кругов.
И это как раз и сходится с их соотношением скорости. 7 кругов ведь на 75% больше, чем 4 круга. Всё правильно, Федя ведь ездит на 75% быстрее, а значит, он и должен проехать не 4 круга, как Женя, а 7 кругов!
Значит, наше предположение верно. К четвёртой встрече Женя проходит четыре полных круга, а стало быть, она приходит к начальной метке, которую мы отметили в месте первой встречи, т.е. место четвёртой встречи совпадает с местом первой встречи. Дальнейшие встречи станут совпадать со встречами в первом цикле рассуждений. Таким образом, всего существует 3 разных места, где Федя обгоняет Женю.
Так же, эту задачу можно решить и «аналитически», через введение неизвестного параметра скорости, и рассмотрения относительной скорости участников, т.е. скорости сближения.
Пусть скорость Жени равна

Тогда скорость Феди равна

Когда Федя догоняет Женю, их скорость сближения равна

(вычитаем, поскольку Женя уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Иначе можно сказать, что скорость Жени в

раза больше, чем скорость сближения, поскольку

Когда Федя в очередной раз обгоняет Женю, его удалённость от Жени, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Жени, Женя пройдет по круговой дорожке в

раза большее расстояние, поскольку её скорость в

раза больше скорости сближения.
Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Женя проходит круг и ещё треть круговой дорожки. Значит за 3 дополнительные встречи (после первой начальной) она и пройдёт полный круг, вернувшись к начальной метке. Т.е. всего существует 3 места, в которых малыш Федя обгоняет пешую Женю.
О т в е т : (б) в 3 точках.