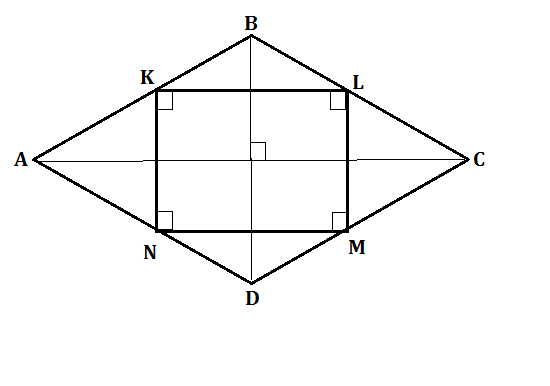
Пусть данный ромб будет АВСD, а четырехугольник, вершинами которого являются середины его сторон, KLMN.
Ромб диагоналями делится на треугольники:
АВС, СDА, АВD, DBC,
Т.к. K, L, M, N - середины сторон этих треугольников, то
KL =MN=AC/2,
KN=LM=BD/2
Площадь ромба равна половине произведения его диагоналей, ⇒
S=d×D:2 (d и D- меньшая и большая диагональ ромба).
d×D:2=48
Так как диагонали ромба пересекаются под прямым углом, а стороны KLMN параллельны им, то KLMN- прямоугольник.
Площадь прямоугольника равна произведению его сторон:
S KLMN=KL×MN
S KLMN=(AC/2,)×(BD/2 )=AC×BD/4⇒
S KLMN=48/2=24см²