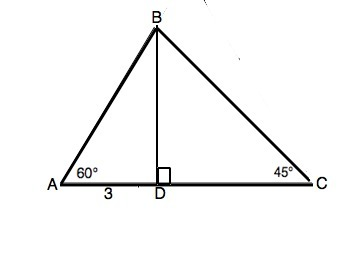
BD⊥AC, ⇒∆ ABD и CBD прямоугольные, их катет DB - общий.
Угол А=60°.
Из ∆ АВD катет BD=AD·tg60°=3·√3
В ∆ ВСD острый угол при вершине С=45°, следовательно,
ВС=BD:sin45°=3√3):√2/2=3√6
Ответ: ВС=3√6
-----------
Задачу можно решить немного иначе. Известно, что катет, противолежащий углу 30°, равен половине гипотенузы.
Угол АВD=90°-60°=30°. Тогда
AB=2AD=6. Далее по т.Пифагора находится BD. Затем из равнобедренного ∆ CBD также по т.Пифагора – ВС.