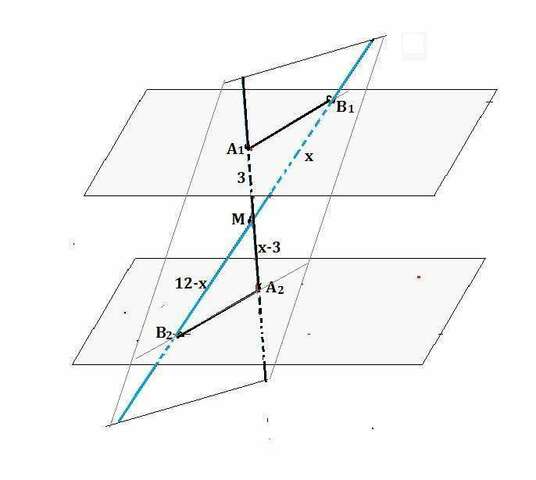
Прямые А1А2 и В1В2 пересекаются, следовательно, через них можно провести плоскость.
А1В1 и В2А2 - линии пересечения этой воображаемой плоскости с данными параллельными плоскостями, поэтому они параллельны ( свойство).
Отсюда в треугольниках А1МВ1 и В2МА2 имеется по три равных угла - вертикальный при М и накрестлежащие углы при параллельных А1В1 и А2В1 и секущих А1А2 и В1В2.
Следовательно, эти треугольники подобны.
По условию А1А2=МВ1
Пусть МВ1=х
Тогда МВ2=12-х
МА2=х-3
Из подобия треугольников следует отношение
МВ1:МВ2=МА1:МА2
х:(12-х)=3:(х-3)
х²-3х=36-3х
х²=36 х=6 см ⇒
МА2=6-3=3 см,
МВ2=12-6=6 см