ПОМОГите, плииииииииииииииииз , геометрия 7 клааааас, только прошу решите,...

Question

ПОМОГите, плииииииииииииииииз , геометрия 7 клааааас, только прошу решите, СРООЧНО

1) В треугольнике ABC известны стороны: AB=4√3, BC=7, СА=2√5. Какой угол в этом треугольнике является наибольшим, а какой наименьшим?

2) 2 окружности касаются друг друга в точке А. Через точку А проведена прямая, касающая одной из окружностей. Докажите, что эта прямая касается также и другой окружности

Answer 1

1. против большей стороны лежит больший угол

7>4√3>2√5 ⇒ BC>AB>CA ⇒ угол A > угла С >угла B

 

2.

Две окружности называются касающимися, если они имеют единственную общую точку, называемую точкой касания.

Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.

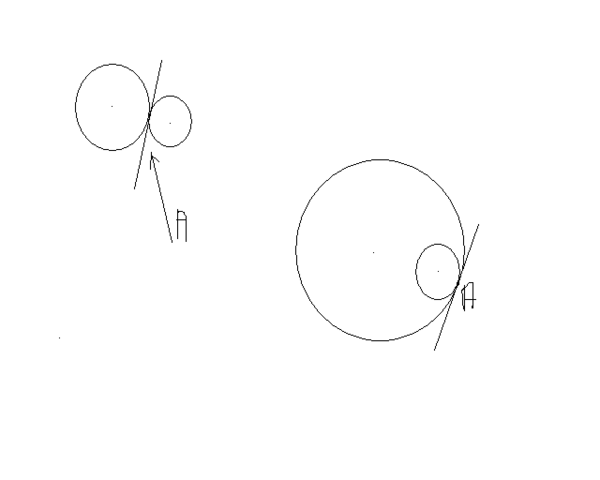
При этом касание двух окружностей называется внешним, если центры окружностей лежат по разные стороны от точки касания и внутренним – если по одну сторону

Если две окружности касаются внутренним образом, то к ним можно провести только одну внешнюю касательную, проходящую через их точку касания (точку А)

Если имеет место внешнее касание двух окружностей, то к ним можно провести три общие касательные – две внешние и одну внутреннюю- в нашем случае как раз ту которая проходит через точку касания A.

 

По условию точка A является общей точкой касания окружностей. ⇒ принадлежит как одной так и другой окружности. Так как касательная проходит через общую точку, то след-но она будет касательной для обеих окружностей.

 

---